- Komplexe Zahlen
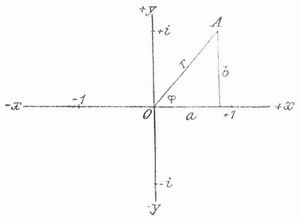
Komplexe Zahlen (komplexe Größen), Zahlen, die aus mehreren nicht durch einander meßbaren Einheiten (s. Einheit) zusammengesetzt sind. In diesem Sinn ist z. B. die Summe aus 3 Äpfeln und 2 Birnen eine komplexe Zahl. In der Mathematik hat man sich zur Einführung komplexer Zahlen dadurch genötigt gesehen, daß gewisse Aufgaben, wie z. B. die Ausziehung einer Quadratwurzel aus einer negativen Zahl nicht lösbar sind, sobald man bloß positive und negative Zahlen zuläßt. Es stellte sich aber heraus, daß man alle diese Aufgaben lösen kann, sobald man die Quadratwurzel aus einer einzigen negativen Zahl (dazu wählte man die aus -1, und allmählich bürgerte sich für √-1 das Zeichen i ein) hinzunimmt und die Rechnungsregeln der positiven und negativen Zahlen auch auf die mit Hilfe von i zu bildenden Zahlen überträgt, wobei dann immer i2=(√-1)2durch -1 zu ersetzen ist. Diese neuen Zahlen nannte man früher unmögliche Zahlen, jetzt nennt man sie imaginär (gedacht, eingebildet), daher auch das Zeichen i, und bezeichnet ihnen gegenüber die positiven und negativen Zahlen als reell (wirklich). Dementsprechend heißt 1 die reelle Einheit und i die imaginäre Einheit. Jede Zahl, zu der man auf diesem Wege durch Addition, Multiplikation und Division gelangt, kann auf die Form a+ib gebracht werden, wo a und b reelle Zahlen bedeuten, und man nennt die Zahlen von dieser Form schlechthin k. Z. oder auch gewöhnliche oder gemeine k. Z. Ist b gleich Null, so hat man es mit einer reellen Zahl zu tun, ist a gleich Null, ohne daß b auch verschwindet, mit einer sogen. rein imaginären Zahl. Die Zahl a-ib nennt man die zu a+ib konjugierte komplexe Zahl und beide zusammen konjugierte k. Z. Gleich Null werden kann eine komplexe Zahl a+ib dann und nur dann, wenn a und b beide verschwinden, denn aus a+ib=0 folgt a=-ib, also ist auch a2=(-ib)2=i2.(-b)2 = i2.b2=-b2, wäre nun eine der beiden Zahlen a2 und b2 von Null verschieden, so wäre sie positiv und daher diese Gleichung unmöglich, folglich sind a2 und b2 beide gleich Null und demnach auch a und b. Hieraus ergibt sich noch, daß zwei k. Z. a+ib und c+id dann und nur dann einander gleich sind, wenn a=c, b=d ist, denn aus a+ib=c+id folgt: a-c+i(b-d)=0, also a-c=b-d=0. Durch die Einführung dieser komplexen Zahlen hat die Mathematik ein Zahlengebiet gewonnen, das in sich abgeschlossen ist und keiner Erweiterung mehr bedarf. Alle Aufgaben, welche die Algebra stellen kann, sind innerhalb dieses Zahlengebiets lösbar, denn es gilt der zuerst von Gauß bewiesene Fundamentalsatz der Algebra, daß jede algebraische Gleichung (s. d.), deren Koeffizienten beliebige k. Z. sind, so viele k. Z. zu Wurzeln hat, wie ihr Grad angibt. Auch die höhere Analysis und die Funktionentheorie haben bisher nirgends eine nochmalige Erweiterung des Zahlengebiets nötig gemacht. Im 18. Jahrh. rechnete man zwar schon mit den komplexen Zahlen, betrachtete sie aber mehr als ein bloßes Hilfsmittel der Rechnung, ohne sie eigentlich als wirkliche Zahlen anzuerkennen. Als solche allgemein anerkannt sind sie besonders durch den Einfluß von Gauß, der auch ihre geometrische Deutung zum Allgemeingut der Mathematiker gemacht hat, obgleich diese Deutung schon vor ihm von andern gegeben worden ist, am frühesten wohl von dem Norweger Kaspar Wessel (1745–1818) in einer 1799 erschienenen, aber unbeachtet gebliebenen Arbeit (Schriften der Kopenhagener Akademie, neue Sammlung, Bd. 5, 1799). Die geometrische Deutung besteht darin, daß man die komplexen Zahlen a+ib durch die Punkte einer Ebene, der sogen. komplexen Zahlenebene, darstellt, und zwar benutzt man dazu zwei durch einen Punkt O gehende auseinander senkrechte gerade Linien als Koordinatenachsen (s. Koordinaten) und deutet a als die Abszisse, b als die Ordinate eines Punktes. Auf diese Weise wird jede komplexe Zahl a+ib durch einen Punkt A mit den Koordinaten a, b dargestellt, und umgekehrt stellt jeder Punkt der Ebene eine komplexe Zahl dar (ist Bildpunkt einer komplexen Zahl), nämlich wenn x und y seine Koordinaten sind, die komplexe Zahl x+iy. Der Punkt O stellt die komplexe Zahl 0+i0 = O dar und heißt daher der Nullpunkt der komplexen Zahlenebene.
Die Punkte der Abszissenachse -x, O, +x stellen die komplexen Zahlen dar, deren imaginärer Teil i. b verschwindet, also die reellen Zahlen, die Punkte der Ordinatenachse -y, O, +y stellen die rein imaginären Zahlen dar (vgl. in der Figur die Bildpunkte der Zahlen +1, -1, +i, -i). Hat man zwei verschiedene k. Z. a+ib und a'+ib', so wird deren Summe (a+ib)+(a'+ib')=a+a'+i(b+b') ebenfalls durch einen Punkt dargestellt, den man aus den Bildpunkten von a+ib und a'+ib' leicht konstruieren kann. Dasselbe gilt von dem Produkte: (a+ib)(a'+ib')=aa'-bb'+i(ab'+ba'). Hierauf beruht die sogen. geometrische Addition und Multiplikation der Punkte der komplexen Zahlenebene. Die Entfernung O A, die der Bildpunkt der komplexen Zahl a+ib von dem Nullpunkt O hat, heißt der Modul oder der absolute Betrag der Zahl a+ib und wird mit mod. (a+ib) oder |a+ib| bezeichnet; nach dem pythagoreischen Satz ist dann; |a+ib|=+√(a2+b2), wo der Quadratwurzel das positive Vorzeichen zu geben ist. Der Ausdruck a2+b2 selbst, die Norm von a+ib, ist gleich dem Produkt der beiden konjugierten komplexen Zahlen a+ib und a-ib. Für reelle Zahlen, wo b=0 ist, fällt der absolute Betrag |a| mit dem sogen. absoluten Werte der reellen Zahl a zusammen, d. h. mit der positiven Zahl, welche die Größe der Zahl a ausdrückt, ohne auf das positive oder negative Vorzeichen von a Rücksicht zu nehmen. Den Winkel φ, den O A mit der positiven Seite der Abszissenachse bildet, nennt man die Amplitude der komplexen Zahl a+ib; setzt man |a+ib|=r, so ergibt sich (s. Trigonometrie) a=rcosφ, b=rsinφ, also a+ib=r(cosφ+isinφ)=reiφ (s. Exponentialfunktion). Diese Form heißt die Normalform der komplexen Zahl a+ib und ist für manche Zwecke besonders bequem. Die Einführung und grundsätzliche Verwertung der komplexen Zahlenebene ist durch Cauchy und Riemann eines der hauptsächlichsten Hilfsmittel der modernen Funktionentheorie (s. Funktion) geworden. Obwohl die gemeinen komplexen Zahlen allen Bedürfnissen der heutigen Mathematik genügen, hat man doch noch allgemeinere k. Z. betrachtet, die mehr als zwei, ja beliebig viele nicht durcheinander meßbare Einheiten enthalten. Das bekannteste Beispiel sind die Hamiltonschen Quaternionen (s. d.), ein andres die von H. Graßmann (s. d.) benutzten alternierenden Zahlen; doch kann man mit allen diesen Arten von komplexen Zahlen, die man wohl auch hyperkomplexe Zahlen nennt, nichts machen, was man nicht auch mit den gewöhnlichen komplexen Zahlen machen kann, sie können nur dazu dienen, gewisse Betrachtungen und Rechnungen zu vereinfachen. Genaueres über die gewöhnlichen komplexen Zahlen findet man in jedem bessern Lehrbuche der Differentialrechnung (s. d.). Über die allgemeinen komplexen Zahlen vgl. H. Hankel, Vorlesungen über k. Z. (Leipz. 1867), und Study, Artikel »Komplexe Zahlen« in Bd. 1 der »Enzyklopädie der mathematischen Wissenschaften« (das. 1904).
http://www.zeno.org/Meyers-1905. 1905–1909.