- Landkarten
Landkarten (hierzu Tafel »Landkartendarstellung«), verkleinerte Abbildungen größerer Stücke der Erdoberfläche. Sie unterscheiden sich von den Plänen, die nur kleine Stücke der Erdoberfläche in großen Maßstäben darstellen, und von den Seekarten (s. d.), bei denen nicht das Land, sondern die dasselbe umgebenden Ozeane und Meeresteile den Hauptgegenstand bilden. Ebenso trennt sie ihr Name von den astronomischen Karten (Sonnensystem, Planeten etc.) und den Sternkarten (s. d.), wenn auch solche Darstellungen gewöhnlich Bestandteile jener Kartenzusammenstellungen sind, die man mit dem Ausdruck Atlanten bezeichnet. Die L. lassen sich in viele Abteilungen bringen, je nachdem man sie nach ihrem Hauptinhalt oder nach ihren besondern Bestimmungen oder nach ihrer Ausführung oder nach Maßgabe ihrer verjüngten Maßstäbe (dem Verhältnis der Zeichnung zur Natur) ordnet. In ersterer Beziehung unterscheidet man: hydrographische oder Gewässerkarten, auf denen Ströme, Flüsse, Bäche, Kanäle, Seen, Teiche erscheinen, mit Angabe der Flößbarkeit und Schiffbarkeit, der Stromschnellen, Brücken, Fähren etc.; orographische oder Gebirgskarten, die vorzugsweise der Darstellung der Unebenheiten des Bodens gewidmet sind und, wenn sie kotierte Angaben der absoluten Höhe der Gipfel, Sättel, Rücken, Pässe etc. und Horizontalkurven gleicher absoluter Höhe (Isohypsen) enthalten, hypsometrische Karten genannt werden; ferner geologische Karten (s. d.), welche die Zusammensetzung des Bodens aus den verschiedenen Gesteinsgattungen zur Anschauung bringen; physikalische Karten über die Erscheinungen in der Wasserhülle der Erde (Ebbe und Flut, Strömungen, Temperatur etc.) und im Luftkreis, z. B. Wärmeverbreitung, veranschaulicht durch die Linien gleicher Jahres-, Monats-, Tagestemperatur (Isothermen), Winde, Luftdruck (Isobaren), Regenverteilung u. dgl.; naturgeschichtliche Karten über die Verbreitung der Pflanzen und Tiere; ethnographische Karten mit Angabe der Wohnsitze und der Verbreitung der Völkerschaften; politische Karten zur Darstellung der verschiedenen Staaten und deren administrativer Einteilung; statistische Karten über alle Zweige der Volkswirtschaft, Produkten-, Industrie-, Forst-, Volksdichtigkeitskarten; Verkehrskarten, zerfallend in Eisenbahn-, Straßen-, Telegraphen- und Postkarten; endlich historische Karten, welche die Veränderung der staatlichen Verhältnisse im Laufe eines gewissen Zeitabschnittes für einen gegebenen Erdraum oder ähnliches vor Augen stellen. Eine besondere Klasse bilden die Schulkarten, die von den Handkarten (für das höhere Studium und zum Geschäftsgebrauch) durch zweckmäßige Beschränkung und Anordnung des Inhalts sich unterscheiden, gleichviel, ob sie als Teil der Schulatlanten für die Schüler oder als Wandkarten (stumme oder beschriebene) für die Schule dienen.
Ein Hauptunterscheidungsmerkmal liegt in der Größe des Maßstabes oder des Verhältnisses der Zeichnung zur Natur, weil hiervon die Reichhaltigkeit der durch die eigentümliche Zeichensprache der L. angedeuteten Gegenstände abhängt. Je größer der Maßstab ist, desto ausführlicher kann sich die Darstellung auf alle ausdrückbaren Gegenstände erstrecken; je stärker die Verkleinerung ist, desto mehr muß die Zahl der Gegenstände auf die Auswahl der für den jedesmaligen Zweck der Karte wichtigsten beschränkt werden. Man kann in dieser Hinsicht eine Einteilung der L. in drei Gruppen vornehmen: 1) Pläne und Flurkarten im Maßstab von 1:500 bis 1:10,000 (Katasterkarten, Pläne zu technischen Zwecken, wie Eisenbahn- und Kanalanlagen, Stadtbebauung etc.); 2) topographische Spezialkarten im Maßstab von 1:10,000 bis 1:200,000 (topographische Landesaufnahmen, Karten zu militärischen und Verwaltungszwecken, zu geologischen Untersuchungen etc.); 3) Generalkarten und geographische Karten im Maßstab von 1:200,000 bis zu dem kleinsten (Spezial- und Übersichtskarten zur speziellen und allgemeinen Orientierung, zum geschäftlichen, touristischen und wissenschaftlichen Handgebrauch, Schulkarten etc.). Es versteht sich von selbst, daß die Abgrenzung zwischen diesen Gruppen nicht mathematisch streng sein kann, daß vielmehr jede Karte mittlern Maßstabes, je nachdem sie in Beziehung zu einer höhern oder niedern Klasse gesetzt wird, als Generalkarte oder als Spezialkarte gelten kann. Sieht man von den Karten der ersten Gruppe ab, die ihrer Natur nach hier weniger in Betracht kommen, so sind es zunächst die topographischen (»ortsbeschreibenden«) Spezialkarten, die vermöge ihres großen Maßstabes, der sich am häufigsten zwischen 1:25,000 und 1:100,000 bewegt, das verläßlichste Bild der Erdoberfläche bieten (vgl. Tafel »Landkartendarstellung«, Karton I u. II). Man verlangt von ihnen, daß sie nicht nur ein genaues Bild der natürlichen Bodenbeschaffenheit (die Formen der Erhebung, die Umrisse der Gewässer etc.) geben, sondern auch alle Dinge enthalten, die auf Besiedelung und Bodenkultur, Kommunikation etc. sich beziehen (Wohnorte im Grundriß, Bahnen, Straßen, Wälder, Felder, Weingärten, Wiesen, Weiden etc.). Sie beruhen auf einer mit allen Hilfsmitteln der Geodäsie ausgeführten trigonometrischen Vermessung, mit der auch die Berechnung zahlreicher absoluter Höhen von Gipfeln, Sätteln, Talpunkten, Wasserspiegeln der Seen etc. verbunden ist. Solche Karten bestehen aus vielen genau aneinander stoßenden Blättern, so daß die Beilage eines Gerippes zur Erläuterung ihrer Zusammensetzung nötig wird. Näheres über die Entstehung und Herstellung der topographischen Karten (Generalstabskarten) s. Landesaufnahme. Bei den Generalkarten, mit welcher Bezeichnung man, gegenüber den topographischen Spezialkarten, L. im Maßstab von 1:200,000 bis 1:500,000 zu belegen pflegt, tritt schon der Fall ein, daß aus Mangel des nötigen Raumes und aus Rücksicht auf Deutlichkeit und Lesbarkeit nicht mehr alle Gegenstände (z. B. Häuser bei zerstreuten Wohnorten, kleinste Bäche, Feld- und Waldwege, Kulturunterschiede, mit Ausnahme größerer Waldstrecken etc.) aufgenommen werden können und eine grundsätzliche Beschränkung eintreten muß; selbst die natürlichen Formen der Bodenerhebung können nicht mehr vollständig ausgedrückt werden (Karton III und IV). Es geht daher der individuelle Charakter allgemach in einen allgemeinen Typus, in eine Charakteristik der Erhebungen im großen über. In noch höherm Maße macht sich diese durch die Verkleinerung des Maßstabes bedingte Ausscheidung an Einzelheiten und Vereinfachung des Ausdrucks, die »Generalisierung«, bei den geographischen Karten, bei denen die Verkleinerung bereits eine halbe Million überschreitet, geltend.
Hier tritt an Stelle des Naturbildes mehr und mehr eine Symbolisierung der topographischen und geographischen Objekte; es erscheinen nur noch Charakterzeichen für alle Wohnorte (Städte, Flecken, Dörfer etc.). Weiler und kleinere Dörfer müssen in volksdichten Gebieten wegbleiben, ebenso minder wichtige Straßen, alle Kulturangaben etc., so daß L. kleinsten Maßstabes nur noch ein abstraktes Bild der allgemeinsten Verhältnisse, der Umrisse, Flächenräume und Erhebungen, geben. Für viele Länder wird ein Blatt genügen, und man kann im allgemeinen sagen, daß der Inhalt der L. im Verhältnis der Quadrate der Maßstäbe abnimmt. Das auf den Inhalt der Karten so einflußreiche Verhältnis der Zeichnung zur Natur (Maßstab oder Reduktionsverhältnis) wird durch Beifügung der numerischen Angabe (z. B. 1:100,000, 1:200,000) und eines oder mehrerer verjüngter Wegemaßstäbe (Kilometer, Meilen etc.) ausgedrückt. In Fällen, wo die zahlenmäßige Angabe des Reduktionsverhältnisses fehlt, läßt es sich mit Leichtigkeit feststellen. Am einfachsten geschieht dies durch einen Maßstab (Fig. 1), einen sogen. Kartometer, der mit dem einen Endpunkt, wo das Unendlichkeitszeichen (∞) steht, an den mittlern Meridian einer Karte bei dem Durchschnitt eines Parallelkreises angelegt wird, und auf dem an der Stelle des Durchschnitts des nächsten Parallelkreises die Verhältniszahl abgelesen werden kann.
Landkartenprojektionen.
Die Schwierigkeit, die allseitig gekrümmte Kugeloberfläche der Erde auf einer Ebene annähernd genau auszubreiten, tritt desto mehr hervor, je größer das Stück der Erdoberfläche ist, das in den Rahmen der Karte fällt; erstere wenigstens nach der einen Seite hin nach Möglichkeit zu mindern, projiziert man diese zunächst auf eine einseitig gekrümmte Fläche, z. B. einen Kegelmantel. der sich dann leicht und ohne Verzerrung in einer Ebene aufrollen läßt. Man denkt sich zu dem Zweck um die Erde einen Kegel gelegt, der das abzubildende Stück in seinem Mittelparallel berührt, und dessen Spitze in der verlängerten Erdachse liegt. Auf dem Kegelmantel erscheinen dann, von der Spitze auslaufend, die Meridiane als gerade konvergierende Strahlen, die die konzentrischen, kreisförmigen Parallelen, deren Mittelpunkt ebenfalls in der Kegelspitze liegt, rechtwinklig schneiden (I. normaler, konischer Entwurf). Je näher der Berührungskreis dem Äquator liegt, desto spitzer wird der Kegel, desto mehr rückt seine Spitze von der Erdoberfläche weg, bis er, wenn der Berührungskreis mit dem Äquator zusammenfällt, ins Unendliche rückt und somit der Kegel in einen Zylinder übergeht, auf dem sich die Meridiane als parallele Geraden abbilden, die sich wiederum mit den Breitenparallelen in rechten Winkeln schneiden, so daß beide Liniensysteme nach der Ausbreitung des Zylindermantels auf einer Ebene geradlinig und rechtschnittig erscheinen (II. normaler, zylindrischer Entwurf). Umgekehrt, je mehr sich der Berührungskreis des Kegelmantels dem Pol nähert, desto stumpfer wird der Winkel an der Spitze des Projektionskegels, desto stärker konvergieren die Meridiane, bis sein Mantel im Pol selbst zur Ebene wird. Die Meridiane schneiden sich dann unter ihrem wahren Winkelwert (Azimut) im Pol, und die Breitenparallelen erscheinen als konzentrische Kreise um den Erdpol (III. normaler, azimutaler Entwurf).
In Fällen, wo Gestalt und Lage des abzubildenden Erdstückes eine normale (polständige) Abbildungsart nicht vorteilhaft erscheinen lassen, kann man die Projektionsfigur nach Erfordernis verrücken, so daß ihre Achse zwischen Erdachse und Äquatorebene oder in letztere selbst zu liegen kommt; im erstern Fall erhält man dann zwischenständige oder schiefachsige, im letztern äquatorständige oder transversale Entwürfe.
Auf dem Globus schneiden sich alle Richtungslinien unter ihren wahren Winkelwerten; sie müssen gewahrt werden, sollen die Umrisse der Länder etc. in ihrer Gestalt unverändert, konform oder winkeltreu bleiben. Das läßt sich nur erreichen, wenn man auf das richtige Verhältnis der Räume und Dimensionen verzichtet, und umgekehrt muß man sich die Verzerrungen der Gestalt gefallen lassen, wenn das Arealverhältnis dem auf der Kugel gleichen soll (Äquivalenz, Flächentreue). Es sind viele Versuche gemacht worden, Gradnetze zu entwerfen, die entweder die Flächentreue oder die Winkeltreue bewahren, sowie solche, die, einen Mittelweg wählend, die Nachteile beider Arten auf ein Minimum zu beschränken suchen, indem sie weder ausschließlich auf Winkeltreue mit Vernachlässigung jeder andern wünschenswerten Eigenschaft, noch ausschließlich auf die Flächentreue zum Nachteil der Winkeltreue Rücksicht nehmen, sondern die unvermeidlichen Abweichungen und Fehler durch Verteilung verringern und von bestimmten Gesichtspunkten aus regeln. Die Gradnetzentwürfe (Projektionen) teilen sich demnach innerhalb jener drei Gruppen, der konischen, zylindrischen und azimutalen Entwurfsarten, in a) orthomorphe, konforme oder winkeltreue, b) in äquivalente oder flächentreue und c) in solche, die weder winkeltreu noch flächentreu sind, sondern irgend eine andre charakteristische Eigenschaft haben; zu diesen letztern zählt auch die wichtige Klasse der vermittelnden oder ausgleichenden. Je nachdem man nun den Entwurfsarten I-III die unter a bis c aufgeführten Eigenschaften verleiht, erhält man winkeltreue, flächentreue etc. konische, zylindrische und azimutale Entwürfe. Bei allen bildet das Meridiansystem das feste, unabänderliche Gerüst, gewissermaßen den Auszug des Gewebes, und nur das System der Breitenparallelen, der Einschlag des erstern, verschiebt sich nach den Gesetzen, die die Winkeltreue, Flächentreue und andre Eigenschaften bedingen. Eine neue Art von Gradnetzen entsteht, wenn man auf den Breitenparallelen der normalen, gleichabständigen azimutalen, konischen und zylindrischen Entwürfe die Längengrade nach ihren wahren Größenverhältnissen aufträgt und die Schnittpunkte miteinander verbindet. Man erhält dann für die Meridiane transszendente Kurven und flächentreue Verhältnisse der Netzmaschen. Breusing hat diese Gruppe sehr charakteristisch als abweitungstreue Netze bezeichnet (Abweitung, das Linearmaß eines Bogens auf einem Breitenparallel). Die abweitungstreuen konischen und zylindrischen Entwürfe beherrschen noch heutzutage unsre sämtlichen ältern Atlanten und geographischen L. Nachfolgend mögen die in unsern Atlanten bisher vorwiegend gebräuchlichen Entwurfsarten näher betrachtet werden.
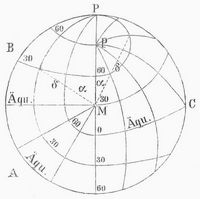
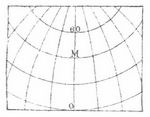
Azimutale Entwürfe. Zieht man vom Mittelpunkt M (Fig. 2) eines abzubildenden Gebietes auf dem Globus nach allen Schnittpunkten des Gradnetzes Strahlen in der Richtung der größten Kreise, so erhält man ein System von Polarkoordinaten für den Punkt M als Projektionspol. Die Lage der so an M angeschlossenen Punkte ist dann bestimmt durch das Azimut α (den Winkel, den die Strahlen mit dem Nordast des Meridians von M bilden) und durch die sphärische Länge der erstern, δ, die gleich den entsprechenden Bogenstücken der Mittelpunktgroßkreise sind.
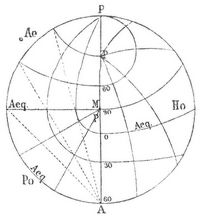
Überträgt man diese Polarkoordinaten im verjüngten Maßstabe auf die Karte, so erhält man den einfachsten azimutalen Entwurf, bei dem die Kartenfläche die Berührungsebene im sphärischen Mittelpunkt der abzubildenden Kugelkalotte ist, und in dem alle Entfernungen, vom Mittelpunkt M aus gemessen (jedoch auch nur von diesem aus), richtige Verhältnisse ergeben, während nach außen hin die Dimensionen in der peripherischen Richtung um so mehr wachsen, je größer die dargestellte Kalotte wird. – Man bezeichnet diesen Entwurf als speichen- oder mittabstandstreu. Als polständiger oder normaler Entwurf, mit M im Pol (Fig. 2 A), findet er sich meistens bei den Polarkarten unsrer Atlanten im Gebrauch; als äquatorständiger oder transversaler, mit M im Äquator (Fig. 2 B), wie als zwischenständiger oder schiefachsiger Entwurf (Fig. 2 C) eignet er sich zur Zeichnung von Kalotten, die sich gleichmäßig nach allen Seiten hin abrunden, wie auch für Halbkugelkalotten oder Planigloben.
Will man einen winkeltreuen azimutalen Entwurf, so sind die Strahlen δ nach der Formel 2tgδ/2 zu verändern, wobei δ den Winkelwert der sphärischen Entfernung bezeichnet. Man gelangt so zu der in den ältern Lehrbüchern als stereographische Projektion bezeichneten Entwurfsart, die als äquatorständiges Netz (Fig. 311) noch heute in ältern Atlanten bei den Planigloben der Erde und als zwischenständiger Entwurf (Fig. 3 C) bei ältern Darstellungen der Land- und Wasserhalbkugeln häufig im Gebrauch ist. Sie gewährt den Vorteil, daß alle Kreise des Kugelnetzes wieder durch Kreise dargestellt werden, deren Mittelpunkte leicht aufzufinden sind, so daß sie leicht konstruierbar ist; indessen vergrößern sich bei ihr die Flächen nach außen hin so, daß sie am Rande einer Hemisphäre das Vierfache jener im Mittelpunkt erreichen. Man kann sie auch aus einer perspektivischen Regel ableiten, indem man den Augenpunkt in einem größten Kreis der Hohlkugel, z. B. bei A (Fig. 3), annimmt und auf die Äquatorebene projiziert.
Kegelprojektionen. Das Prinzip, die Kreise des Gradnetzes auf einen Kegelmantel zu projizieren, rührt von Ptolemäus (150 v. Chr.) her. Die Übertragung findet auf die Mantelfläche eines Kegels statt, der die Erde im mittlern Parallel der Karte berührend gedacht wird.
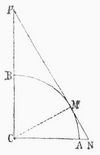
Dem Mittelpunkt M entspricht der Kegel, dessen Hälfte PNC in Fig. 4 gezeichnet ist. Vom Punkt P aus, dessen Entfernung man durch die Kotangente (PM) der geographischen Breite A M findet, werden die Parallelkreise gezogen, auf dem mittlern, der durch M geht, die Grade der Länge vom Mittelmeridian aus in ihrem richtigen Größenverhältnis (abweitungstreu) aufgetragen und durch die Durchschnittspunkte von P aus die Meridiane gelegt (Fig. 5). Diese Projektionsart liefert geradlinige Meridiane und konzentrische Parallelkreise. – Aus der Fig. 4 geht unmittelbar hervor, daß die schmale Zone, deren Mitte der Parallelkreis in M bildet, die geringste Verzerrung erleiden muß, weil sie nahezu mit dem Kegelmantel zusammenfällt, daß dagegen die Längengrade in dem Maße wachsen müssen, wie sie sich von jener nach N. und S. hin entfernen. Es eignet sich dieser Entwurf daher nur für solche Karten, deren Längendimension eine westöstliche Richtung hat.
Der vorstehend beschriebene Entwurf ist weder flächentreu noch winkeltreu, sondern nimmt eine vermittelnde Stellung ein. – Gerhard Mercator verbesserte (1554) die Projektion des Ptolemäos, indem er (wie später 1745 de l'Isle) die Längengrade nicht auf dem mittlern Parallel auftrug, sondern zwei in der Mitte zwischen diesem und den Rändern der Karte gelegene Parallelkreise abweitungstreu machte, wodurch die Abweichung der Projektion vom Kugelnetz auf die halbe Fehlergröße verringert wurde.
Dieser, meistens als de l'Isles Schnittkegelprojektion bezeichnete Entwurf verdient seiner vorzüglichen Eigenschaften wegen eine viel häufigere Anwendung, als er bisher gefunden hat, obwohl man ihm nicht selten in den Atlanten begegnet.
Zylindrische Entwürfe. Denkt man sich die Erde oder den Globus in einem Zylindermantel eingeschlossen, der sie im Äquator berührt, und das Meridiansystem wie bei der Kegelprojektion auf diesen übertragen, so muß, wenn er in der Ebene aufgerollt wird, der Äquator als gerade Linie und die Meridiane müssen als senkrechte Parallellinien auf ihm erscheinen. Trägt man nun die Abstände der Breitenparallelen auf diesen so ab, daß bei gleichbleibender Größe der Längengrade die Breitengrade in dem Maße wachsen, daß das Verhältnis zwischen beiden in allen Breiten richtig bleibt, so erhält man den wichtigen winkeltreuen zylindrischen Entwurf, der von Mercator herrührt und nach ihm Mercatorprojektion (Fig. 6) genannt wird.
Da die Längengrade in der Wirklichkeit im Kosinusverhältnis der Breite abnehmen, muß daher das Wachstum der Breitengrade auf der Karte nach dem Sekantenverhältnis erfolgen. Ihre wichtigste Eigenschaft ist, daß die loxodromische Linie, d.h. die Linie, die ein Schiff beim Segeln in stets gleicher Richtung beschreiben würde, eine Gerade wird. Dieser Vorteil hat bewirkt, daß Mercators Erfindung (1569) auf alle Seekarten ausgedehnt wurde. Da sie, obgleich durch die geradlinige Abbildung aller auf der Erde Kreise bildenden Gradnetzlinien jede figürliche Beziehung zur Kugelgestalt bei ihr verloren geht, die einzige wirklich brauchbare Projektion ist, die eine konforme Abbildung der ganzen Erdoberfläche, mit Ausnahme der den Polen zunächst gelegenen Teile, im Zusammenhang zuläßt, wird sie auch sehr häufig bei Erdkarten und namentlich bei solchen zu physikalisch-geographischen Darstellungen angewandt. Die starke Vergrößerung in den hohen Breitengraden ist ein unvermeidlicher Übelstand, der aber nicht so schwer wiegt wie die Verzerrung der Konturen bei andern Projektionen der ganzen Erdoberfläche. Es gibt auch einen flächentreuen zylindrischen Entwurf, wie einen solchen mit gleichabständigen Parallelen; beide werden jedoch nur selten verwendet.
Abweitungstreue Entwürfe. Trägt man auf den Parallelen der einfachen Kegelprojektion (Fig. 6) oder einer Zylinderprojektion mit gleichabständigen Parallelen die Längengrade nach ihrem wahren Verhältnis vom Mittelmeridian aus ab, so erhält man diejenigen zwei Entwurfsarten, denen man in unsern Atlanten am häufigsten begegnet.
Die erstere (Fig. 7), deren Grundgedanke auf Ptolemäos zurückzuführen ist, während erst Mercator das strenge Gesetz des Entwurfs in seiner Ausgabe der Ptolemäischen Kartensammlung festgestellt hat, wird fälschlich dem Franzosen Bonne zugeschrieben und noch heute nach ihm benannt; die letztere (Fig. 8), von Mercator herrührend (1606), wird irrtümlich als Sansonsche (1650) oder Flamsteedsche (1729) oder auch als Sanson-Flamsteedsche bezeichnet. Bei beiden Netzen bildet der Mittelmeridian eine gerade Linie, während die seitlichen Meridiane sich um so stärker krümmen, je weiter sie vom mittlern abstehen, so daß die rechtwinkligen sphärischen Trapeze des Netzes, namentlich nach den Kartenecken hin, mehr und mehr eine rhombische Gestalt bekommen und die figürlichen Verzerrungen bei größern Kalotten (Asien, Nordamerika, Afrika) karikaturenhaft werden. Werden die auf dem Mittelmeridian gleichabständigen Parallelkreise nicht konzentrisch gezogen, sondern mit den Kotangenten ihrer geographischen Breite als Radien, und auf ihnen die Längengrade vom Mittelmeridian aus abweitungstreu aufgetragen, so erhält man die polykonische Projektion, eine Entwurfsart, die namentlich bei den Arbeiten der nordamerikanischen Küstenvermessung im Gebrauch ist, aber auch bei Ländern von großer meridionaler und geringer ostwestlicher Ausdehnung (Chile, Ägypten) mit Vorteil angewandt werden kann. Auch die Streifen, aus denen der Globus zusammengesetzt wird, werden nach den Regeln dieser Entwurfsart entworfen. Strengen Anforderungen an Genauigkeit, d.h. an eine der Wirklichkeit entsprechende Übereinstimmung aller Dimensionen in Länge, Breite und Flächeninhalt, kann keine der vorstehend besprochenen Entwurfsarten genügen; bei einigen der neuern Länderaufnahmen, wie bei der von Preußen, der neuen Generalstabskarte des Deutschen Reiches in 1:100,000 und der neuen Spezialkarte der österreichisch-ungarischen Monarchie in 1:75,000, bei denen es sich um eine große Zahl von Kartenblättern handelt, hat man daher zu der schon 1790 von Jäger angewandten Polyederprojektion gegriffen, die sich der Kugeloberfläche vollkommen anschmiegt und bei der der Einfluß der Krümmung der Erdoberfläche so verschwindend klein wird, daß er hinter den zufälligen Unregelmäßigkeiten in der Zusammenziehung des Papiers beim Druck weit zurückbleibt. Wie der Name der Entwurfsart bereits andeutet, wird sie eigentlich auf einem Polyeder und zwar in Gradabteilungskarten projiziert, d.h. man denkt sich das darzustellende Gebiet durch Meridiane und Parallelkreise in so kleine Trapeze geteilt, daß die Abbildung eines derselben in dem gewählten Maßstab auf einem handlichen Papierformat Platz findet.
Fig. 9 stellt das Trapez eines Längen- und Breitengrades vor, das in acht Sektionen zerfällt, deren jede 30 Längenminuten breit und 15 Breitenminuten hoch ist. Die vertikalen Seiten der Sektionen sind sonach Teile von Meridianen, die horizontalen Seiten sind Teile von Parallelkreisen. Jedes der Trapeze ist so klein, daß es als ebenes Viereck angesehen, bez. als mit einer durch seine vier Eckpunkte gelegten Ebene übereinstimmend betrachtet werden kann. Da die Karte im ganzen der Krümmung der Erdoberfläche folgt, läßt sie sich füglich nicht als ebene Abbildung aus den Sektionen zusammensetzen; allein wo es sich nur um eine beschränkte Anzahl von Nachbarsektionen handelt, ist die Abweichung von der Ebene so gering, daß sie in kleinen Abteilungen sehr wohl aneinander gestoßen werden können.
Gebirgs- (Terrain-, Gelände-) Darstellung.
Ein besonderes Augenmerk verdienen die Unebenheiten der Erdoberfläche, und es ist in neuerer Zeit das Bestreben immer reger geworden, dem dritten körperlichen Faktor, der Höhe, ebenso gerecht zu werden wie den Dimensionen der Länge, Breite und Fläche. Wie beim Kugelkörper die Projektion hinter den Anforderungen der Richtigkeit der horizontalen Dimensionen zurückbleibt, so erreicht die beste Zeichnungsmanier nur unvollkommen die Plastik der Natur und das nur bei den topographischen Karten großen Maßes, die mit der charakteristischen Individualität der Erhebungen einigermaßen Schritt halten können. In ältester Zeit begnügte man sich mit den einfachsten Zeichen, um überhaupt Gebirge anzugeben.
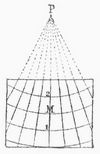
Sägenartige Segmente (Fig. 10) stellen in den ältesten Ausgaben des Ptolemäos die Hochgebirge vor. Die Seitenansicht der Berge ging später in die Haufenform (Fig. 11) über, und diese reicht bis ins vorige Jahrhundert hinein.
Bei topographischen Karten (früher Staatsgeheimnis) konnte diese allgemeine konventionelle Bezeichnungsart nicht genügen; es wurden (in Frankreich zuerst) Höhenschraffen und schiefe Beleuchtung eingeführt, und die verschiedenen »Plankammern« der Staaten zeichneten das Terrain ihrer Aufnahmeblätter nach sehr verschiedenen Schlüsseln, bis der sächsische Major Lehmann (1796) ein auf senkrechte Beleuchtung und auf Böschungswinkel von 5–45° Steigung gegründetes System der Schraffierung aufstellte, das später in Deutschland, Österreich und andern Ländern, wenn auch meist abgeändert, zur Annahme und Geltung gekommen ist. Lehmann wollte damit erreichen, daß man aus dem Verhältnis der Strichdicke zum weißen Zwischenraum den Neigungswinkel auf ca. 5° schätzen könne und daß die Lage der Schraffen den Wasserablauf andeute, indem sie senkrecht auf den Horizontalkurven stehen sollten, die aber nach der Zeichnung wieder entfernt wurden. Wäre er einen Schritt weiter gegangen durch Einführung bleibender absoluter Niveaulinien (Horizontalen, Isohypsen), so würde er der Begründer der in neuester Zeit als wichtigster Bestandteil der Terrainaufnahme erkannten hypsometrischen Karten geworden sein, bei denen, die erreichbare Genauigkeit der Horizontalen vorausgesetzt, das Verhältnis der Entfernung zweier Horizontalen zu ihrem Höhenabstand den Böschungswinkel viel genauer zu bestimmen erlaubt als die wie ein Ideal aufgestellte Schraffentheorie, deren genaue Ausführung lange Übung erfordert (Karton V, VI u. VII).
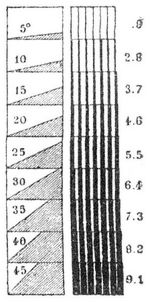
Da aber die Niveaulinien für sich kein Bild gewähren, auch wenn sie mit Höhenzahlen reichlichst ausgestattet sind, und keinen plastischen Eindruck hervorbringen können, so bleibt das Zeichnungsschema Lehmanns noch in Kraft, und es erscheint als Vorteil, das gute Alte mit dem guten Neuen zu vereinigen, indem man dem durch Schraffierung hergestellten Geländebild durch Belassung der Horizontalen ein geometrisch festeres Rippenwerk verleiht. Der Schweizer Kartograph Ziegler hat auf seiner Karte des Kantons St. Gallen (1:25,000) vor etwa 40 Jahren eine Neuerung versucht, indem er jede ausgezogene Schicht von 100 m in nicht ausgezogene 10 Unterschichten von 10 m teilte, die Schraffen aber so stellte, daß sie bei jeder Zwischenschicht absetzten und so auch die nicht ausgezogenen Schichtenlinien sichtbar machten (Fig. 12). Manche Versuche von Verbesserungen des Lehmannschen Systems (z. B. von Müffling) haben das leichtere Erkennen des für militärische Zwecke tauglichen Terrains zum Anhaltspunkt genommen. Eine der rationellsten und das Wesen der Lehmannschen Schraffierungsskala nur unbedeutend beeinträchtigenden Abänderungen besteht in der Ausdehnung auf 50° und Gründung der Verhältnisse von Strichdicke und Zwischenräumen auf das Dezimalsystem (Fig. 13). Die Neigungen des Bodens, die unter 5° betragen, bleiben, wie bei Lehmann, unberücksichtigt; die Dicke der Striche wird, bei gleichbleibendem Abstand ihrer Mitte, für Böschungen von 10° auf das Doppelte, für Böschungen von 15° auf das Dreifache etc. erhöht, u. die volle Schwärze tritt erst bei 50° Neigung ein, also bei einem Grade der Steilheit, der nur bei erdentblößten Felsabhängen vorkommt.
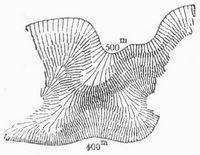
Für die Darstellung alpiner Gebiete hat seit 30–40 Jahren die vom Schweizer General Dufour bei der Bearbeitung der eidgenössischen topographischen Karte der Schweiz in 1:100,000 (der sogen. Dufourschen Karte) mit durchschlagendem Erfolg wieder aufgegriffene und zu neuem Leben erweckte schiefe Beleuchtung mehr und mehr Raum gewonnen. Dufours Manier unterscheidet sich jedoch wesentlich von der ältern französischen dadurch, daß sie die Schraffenlage dem Lehmannschen Grundsatz entsprechend verwendet und verstärkte Schattierungen, bei strenger Durchführung der Beleuchtung aus Nordwesten, lediglich zur Erzielung einer erhöhten plastischen Wirkung benutzt. In Verbindung mit Isohypsen, durch die der Gebirgszeichnung ein scharfer mathematischer Ausdruck verliehen würde, dürfte diese Darstellungsart für alpine Bergformen das denkbar Vollkommenste bieten.
Sieht man von der Bergzeichnung ab und will doch auf hypsometrischen Karten (Schichtenkarten) eine zweckentsprechende Wirkung erzeugen, so muß man sich steigender Töne bedienen, entweder in Einer Farbe oder, wenn man eine auffällige Übersicht des gleich hohen Terrains auf einer Karte erzielen will, in verschiedenen Farben, wobei mehrere Arten bezüglich der Skalenentwürfe in Anwendung kommen können. Der am allgemeinsten anwendbare Grundsatz (System Hauslab) lautet: »Je höher, desto dunkler«. Er hat für sich, daß die hellsten Töne auf das stärker besiedelte Tiefland, die dunkelsten auf den kleinen Raum des Hochgebirges verteilt werden, wodurch jede Störung der Leserlichkeit vermieden wird, die bei dem entgegengesetzen Prinzip (v. Sydow) im Tiefland eintreten kann (Karton VII). Für ozeanische Tiefen verwandelt sich das Gesetz in das unbestrittene: »je tiefer, desto dunkler«. Mittelwege sind versucht worden durch die Verlegung der lichtern Töne in die Mittelstufen des Terrains oder der dunkelsten Töne in das Hochgebirge unter der Schneegrenze. Neuerdings hat K. Peucker eine aus physiologisch-optischen Gesetzen abgeleitete Farbenskala vorgeschlagen, die von Blau (bez. Violett) in der Tiefe beginnend, bis zu Rotbraun für die großen Höhen, zu immer kräftigern Tönen anwachsend, eine plastischere Wirkung ergibt. Aus Schichtenkarten lassen sich durch Ausschneiden und Aufeinanderkleben proportional dicker Kartons Schichtenreliefs bilden, die bei großem Maßstab, wenn die Schichten sehr zahlreich und niedrig sind, wirklichen Reliefs nahekommen.
Zeichnung und Vervielfältigungsmethode.
Die Zeichnung der Landkarte, das Original, wird vom Landkartenzeichner oder Kartographen angefertigt; die Kunst des Landkartenzeichnens nennt man Kartographie. Sie darf, wenn es sich um Entwerfung und Anordnung, nicht um bloße Kopierung handelt, nicht als eine mechanische Arbeit angesehen werden, die nur technische Geschicklichkeit erfordert, sondern der Kartograph muß notwendig zugleich Geograph sein. Sind Größe (Format, Rahmen) und Maßstab der zu zeichnenden Karte festgestellt, so wird zuerst das Gradnetz als das geometrische Gerüst des Entwurfs entworfen (s. oben: Landkartenprojektionen). Den Stoff an sich, der auf der Zeichnung niedergelegt werden soll, liefert die Geodäsie (Feldmeßkunst) in ihren verschiedenen Ergebnissen (topographischen und geologischen Karten, Seekarten, hypsometrischen Messungen, astronomischen Ortsbestimmungen, Routenaufnahmen u.a.m.), während die Geographie mit ihren Hilfsmitteln (Reise- und Länderbeschreibungen, geographischen und Reisehandbüchern, statistischen Werken etc.) die Fingerzeige für die richtige Darstellung bietet. – Sobald das Quellenmaterial vom Kartographen kritisch gesichtet worden ist, beginnt er damit, die Situation (Küstenumrisse, Flußnetz, Verkehrslinien, Grenzen, Ortszeichen und andres Linien- und Punktwerk) in das Gradnetz der Zeichnung und zwar mit Hilfe eines das Augenmaß hinreichend unterstützenden, engmaschigen Netzes von Hilfslinien (1-, 5-, 10- etc. Minutentrapeze) aus freier Hand zu übertragen. Ist mit dieser Arbeit eine Reduktion der Zeichnung von einem beträchtlich größern Maßstab auf einen kleinern verbunden, so verlangt sie, wegen der dabei nötig werdenden kritischen Auswahl sowie veränderten Anordnung des Stoffes zur Erreichung einer richtigen Verallgemeinerung des Kartenbildes, einen den Gegenstand vollständig beherrschenden Kartographen. Aber auch die Abstimmung des Flußnetzes in bezug auf die Stärkeverhältnisse der Linien (dünn an der Quelle, allmählich sich verstärkend nach der Mündung hin), durch die ihre hydrographische und wirtschaftliche Bedeutung zum Ausdruck kommen soll, wie die zweckmäßige Wahl der Signaturen (s. d.) und Symbole für die übrigen Bestandteile der Situation, die je nach Maßstab und Zweck der Karte getroffen werden muß, erfordern neben großer praktischer Erfahrung und tüchtiger zeichnerischer Handfertigkeit unausgesetzte geistige Tätigkeit, umfassendes geographisches Wissen und einen gewissen künstlerischen Sinn. – In gleicher Weise wie die Situation wird die Gebirgszeichnung (Terrain) mit Hilfe des verengerten Maschennetzes in die Zeichnung übertragen. Im allgemeinen findet die Gebirgsdarstellung (s. oben) auf unsern Hand-, Reise- und andern Orientierungskarten, wie in der Mehrzahl der topographischen Kartenwerke, durch Schraffierung statt, indem die Abhänge der Gebirge durch Strichlagen charakterisiert werden; während nun der topographische Zeichner die gesamte Terrainzeichnung dem Terrainstecher Strich für Strich mit der Feder vorzeichnet, so daß dieser ein genaues Vorbild für Lage, Länge, Weite und Stärke der Striche erhält, unterzieht sich der Kartograph bei L. kleinern Maßstabes (für Hand- und Schulatlanten) dieser mühsamen und zeitraubenden Arbeit nicht, sondern erleichtert sich seine Aufgabe dadurch, daß er seine Terrainzeichnung in Tuschmanier mittels brauner oder grauer Töne ausführt. Diese getuschten Zeichnungen in Strichmanier zu übertragen, ist dann die Aufgabe des Terrainstechers. Als drittes Element in der Karte ist die Schrift zu bezeichnen. Sie ist, trotz ihrer engen Beziehung zum Inhalt der Karte, nicht als integrierender Bestandteil des Kartenbildes zu betrachten, sondern nur als erläuternde Zutat, und zwar kann man sie, da sie das erstere mehr oder weniger beeinträchtigt, indem sie es verdeckt, beschwert und in gewissem Maße unklar macht, als ein notwendiges Übel ansehen. Daraus ergibt sich aber die Aufgabe des Kartographen bezüglich des Äußerlichen der Kartenbeschreibung ganz von selbst: Bewahrung der Deutlichkeit und möglichste Schonung des Kartenbildes durch Wahl von zweckmäßigen Schriften in bezug auf Gattung, Größe und Stärke, wohldurchdachte Anordnung der Namen hinsichtlich Stellung und räumlicher Ausdehnung, weises Maßhalten betreffs der Schriftmenge. – Die wissenschaftliche Aufgabe der Schriftbearbeitung findet ihre Angriffspunkte in der dem Zwecke der Karte anzupassenden Auswahl von Namen, in der kritischen Behandlung des sprachlichen Elements (Orthographie etc.) sowie in der Gestaltung des formellen Teiles der Schrift mit steter Rücksichtnahme auf deren Bestimmung: durch ihre Ausdrucksweise die relative Bedeutung der beschriebenen Objekte unmittelbar klar zu machen und so die Auffassung des Kartenbildes zu unterstützen.
Die wichtigste Eigenschaft aller Karten ist die Richtigkeit, worunter nicht bloß eine möglichst erreichbare Korrektheit der Eigennamen, der Zeichen, der Umrisse, sondern auch eine der Wirklichkeit entsprechende Übereinstimmung aller Dimensionen in Länge und Breite und der Flächeninhalte verstanden wird. Gleich strenge Anforderungen stellt man aber auch an die Klarheit, Lesbarkeit und Schönheit einer Karte. Nächst der Eleganz, Sauberkeit und Schärfe des Stiches und Druckes trägt das Kolorit dazu bei, diese Anforderung zu befriedigen. Es soll einerseits das Zusammengehörige in übersichtlicher Weise vereinigen, anderseits aber auch das zu Unterscheidende nach Möglichkeit trennen. Man unterscheidet daher durch zweckmäßige Anwendung verschiedener Farben, z. B. Wasser und Land, Hochland und Tiefland u.a.m., und vereinigt durch die nämliche Farbe (Fläche oder Randkolorit) politisch zusammengehörige Ländergebiete u. dgl. Die Aufgabe des Kartographen ist es, durch sachgemäße und geschmackvolle Wahl der anzuwendenden Farben und ihre harmonische Abstimmung eine dem Auge wohltuende, anschauliche und leicht verständliche Darstellung zu erreichen.
Die verschiedenen Arten der Vervielfältigung haben großen Einfluß auf die Schönheit der äußern Erscheinung der L. sowohl als auch auf die Schnelligkeit und Wohlfeilheit der Erzeugung. In ersterer Beziehung leistet der Kupferstich in bezug auf Schärfe und Tiefe des Striches sowie Weichheit und Feinheit der Ausführung unstreitig das Beste, durch galvanisch erzeugte Hilfsplatten unterstützt, auch in beliebiger Menge; Korrekturen sind nicht schwierig auszuführen, namentlich auf den Hochplatten (Matrizen), doch erfordern sie mehr Zeitaufwand und Kosten. Billiger erzeugt die Lithographie in Verbindung mit dem gegenwärtig hochentwickelten lithographischen Schnellpressendruck, der namentlich die weitestgehende Ausnutzung von farbigem Druck gestattet. Neuerdings hat auch die Lithographie in Verbindung mit der Buchdruckpresse glänzende Erfolge erreicht, indem lithographisch gravierte Karten durch Überdruck auf Zink (Chemigraphie oder Zinkographie) in Hochdruckplatten verwandelt werden, um in der Buchdruckpresse zur Benutzung zu gelangen. Auch bei dieser Art der Vervielfältigung kann farbiger Druck in ausgedehntestem Maße zur Verwendung kommen, doch ist das Verfahren nur bei sehr großen Auflagen von Vorteil, da umfassendere Korrekturen stets eine Erneuerung der Druckplatten erforderlich machen. Der Stahlstich eignet sich für sehr große Auflagen von der Mutterplatte, wird aber, seitdem der Kupferstich sich die Galvanoplastik dienstbar gemacht hat, der Schwierigkeit der Plattenkorrekturen wegen kaum noch angewandt. Der Holzschnitt, im Beginn der Kartographie noch in oftmaliger Anwendung, ist aus ihr infolge der Entwickelung der chemigraphischen Verfahren gänzlich verdrängt worden. Kartenabdrücke jeder Art können auch durch das anastatische Verfahren (s. Anastatischer Druck) reproduziert werden, doch wird man nur noch selten zu ihm greifen, seitdem man mit Hilfe der Photographie in technischer Beziehung weit günstigere Resultate zu erlangen vermag; denn durch Photolithographie, Photozinkographie und Heliographie können Originalzeichnungen unmittelbar auf Stein, Zink oder Kupfer übertragen, auch je nach Wunsch verkleinert oder vergrößert werden. Der Zeit nach reichen Holzschnitt und Kupferstich bis in das letzte Viertel des 15. Jahrh. zurück; die typographische Herstellung von L. ist öfters schon versucht (1478, 1777, 1839, 1862) und wieder verlassen worden; die Lithographie datiert vom Anfang vorigen Jahrhunderts, der Stahlstich von 1820; die andern Erzeugungsarten sind Entdeckungen der jüngsten Jahrzehnte. Über die Fortschritte der Reproduktionstechnik auf dem Gebiete des Kartenwesens berichten fortlaufend die »Mitteilungen des k. u. k. militär-geographischen Instituts« (Wien).
Atlanten.
Eine systematische Zusammenstellung von Karten gleichförmigen Formats nennt man einen Atlas. Ein fester Plan, dessen Grundsätze für alle Karten maßgebend sind, sollte jedem solchen Unternehmen zugrunde liegen. Dieser Plan erstreckt sich 1) auf die Zahl der Karten, ihre Ordnung und ihr Format; 2) auf die Vollständigkeit, damit kein Berücksichtigung verdienendes Land unvertreten bleibt oder im Mißverhältnis zu andern ungenügend bearbeitet erscheint; 3) auf die Maßstäbe, insofern es des bequemen Vergleichens wegen erwünscht ist, wenn gewisse Folgen von Karten (z. B. die Karten der Erdteile, der europäischen Staaten etc.) in gleichgroßem Maßstab entworfen werden oder, wenn Ausnahmen stattfinden müssen, die verschiedenen Maßstäbe unter sich leicht vergleichbar sind (z. B. 1:1 Mill., 1:2 Mill., 1:4 Mill. etc.); 4) auf den Karteninhalt, d.h. auf eine zum Raume verhältnismäßige, dem Hauptzweck des Atlas entsprechende Auswahl des Stoffes im einzelnen, dann eine in den einzelnen Kartenfolgen tunlichst gleichförmige Bezeichnung der Gegenstände (Orte, Bahnen, Straßen etc.); 5) auf die kluge Benutzung verfügbarer Räume zu Spezialdarstellungen (Nebenkärtchen von Hauptstädten, Fabrikbezirken, Pässen etc.); 6) auf die möglichst gleichartige technische Ausführung. Als vorzügliche deutsche Handatlanten sind zu nennen: der von Kiepert (3. Aufl., 45 Bl., Berlin, D. Reimer, etwas veraltet), Debes (3. Aufl., 50 Bl., Leipzig, Wagner u. Debes), Andree (4. Aufl., 93 Bl., Bielefeld u. Leipzig, Velhagen u. Klasing), Stieler (9. Aufl., 100 Bl., Gotha, Justus Perthes), Sohr-Berghaus (9. Aufl., 84 Bl., Glogau, Karl Flemming), sämtlich mit Namenregister versehen; die beiden letzten noch im Erscheinen begriffen.
Geschichtliches.
Die Geschichte der Kartographie hält mit der Entwickelung der Geodäsie und der Geographie als Wissenschaft gleichen Schritt. Man kann vier Perioden unterscheiden: eine der alten Zeit bis ca. 1000 n. Chr., eine des Mittelalters bis zur Entdeckung von Amerika (1492), eine Periode des Fortschritts, die etwa mit 1770 abschließt, und eine der neuen und neuesten Zeit. Aus dem Altertum haben wir nur Sagen, Vermutungen und dürftige Nachrichten über Karten primitivster Art, von denen sich keine Spur erhalten hat (vgl. Erdkunde, S. 7 ff.). Aus den ersten Jahrhunderten unsrer Zeitrechnung stammen die Handzeichnungen von Karten in den ältesten Manuskripten der Kosmographie des Ptolemäos, eine Erdbeschreibung, die eigentlich ein Verzeichnis astronomischer Positionen ist, nach Breite und Länge auf so unsichere Berechnungen basiert, daß die Fehler der zu großen Länge beim Ostende des Mittelländischen Meeres 20°, an der Gangesmündung schon 46° betragen; ferner die Tabula Peutingeriana, eine von W. nach O. unnatürlich verzerrte Straßenkarte des römischen Reiches mit Angabe der Militärstationen und Meilenentfernungen. Der zweiten Periode gehören die verschiedenen Handzeichnungen an, meist von Mönchen herrührend, Versuche sogen. Rad- oder Weltkarten (mappae mundi), auf denen den Irrtümern des Ptolemäos, der noch lange als unfehlbare Quelle galt, durch Mißverstehen der Identität der neuen Entdeckungen eines Marco Polo u.a., die man den alten einfach anreihte, neue hinzugefügt wurden, so daß Asien so weit gegen O. rückte, daß Kathai (China) nur noch 130° westlich von Spanien lag. Zu diesen Weltkarten zählen die Haidinghams (im Dom zu Hereford, 14. Jahrh.), die des Marino Sanuto (1320), die Florentiner Seekarte (1351), die sogen. Katalanische Karte (1375) eines mallorcanischen Schiffers, die Karte des Andrea Bianco (1436), die Weltkarte im Palast Pitti zu Florenz (1447), jene des Fra Mauro in der Markusbibliothek zu Venedig (1453). Der Globus des Nürnberger Gelehrten Behaim von 1492 kann als Schlußstein dieser Periode angesehen werden; er trägt noch alle Spuren des unvollkommenen Wissens und der Irrtümer seiner Zeit.
Im dritten Zeitabschnitt machen sich die Fortschritte der Kartographie schon sehr bemerkbar. Es erscheint eine ansehnliche Anzahl von Kompaß- oder Küstenkarten (portolani), die in Venedig, Genua, Lissabon, Mallorca u.a. O. fast fabrikmäßig gefertigt werden, freilich noch mit teilweise falsch orientierten Umrissen, infolge der Unkenntnis der Mißweisung der Magnetnadel, und mit bedeutenden Fehlern bezüglich der geographischen Länge, die nur nach der Schnelligkeit des Segelns geschätzt wurde. Aus ihnen werden die Weltkarten zusammengesetzt, und es wird die Kunst des Grabstichels zu ihrer Vervielfältigung aufgeboten. Jede größere Bibliothek besitzt eine Anzahl von Portolanen aus jener Zeit. Seltener sind die Weltkarten, sowohl die Handzeichnungen als die Abdrücke der gestochenen. In diese Folge gehören die Carta marina von Portugal (1504), die Weltkarten von Descelliers (1553, im Privatbesitz in Wien), Gaultier (1512), Apian (1524), Ribero (1529), Cabot (1544) u.a., die Globen von Schöner (1520), Mercator (1541) und dessen schon mit vergrößerten Breiten konstruierte Weltkarte (1569). Allgemach vollzieht sich die Emanzipation von Ptolemäos, die Annahme bestimmter Projektionen, die Auswechselung fabelhafter und hypothetischer Ausfüllung mit den Ergebnissen neuer Entdeckungen im Bereich des asiatischen und amerikanischen Kontinents. So wird es möglich, daß vor und nach 1600 an die Stelle der Portolani ganze Atlanten treten, z. B. der von Mercator (gest. 1595), den dessen Söhne vollendeten, von Ortelius (»Theatrum orbis terrarum«, 1570), Hondius (gest. 1611), Jansson (1636, 6 Bde., mit 451 Karten), Blaeuw (gest. 1638) und seinen Söhnen (372 Karten) etc. Damals waren also die Niederländer die Tonangeber im Gebiete der L. In Deutschland sind zu nennen: Homann (gest. 1724) in Nürnberg (etwa 200 Karten), Seutter in Augsburg (Atlas, Wien 1736, 50 Blatt), in Frankreich Tavernier u.a. Der Landkartenstich war, wie der Buchdruck, ein Gewerbe geworden.
Mit Jacques und César Cassini, die 1750–1793 die große Triangulation von Frankreich und die darauf begründete große topographische Karte vollendeten, beginnt endlich die Zeit der genauen topographischen Aufnahmen und der kritischen Bearbeitung der Karten. In ersterer Beziehung steht nun Frankreich an der Spitze; doch genügten die großartigen Leistungen der beiden Cassini nicht, es ward eine neue topographische Karte geplant (1824), deren letzte Blätter (267) 1880 erschienen sind. Dem Beispiel Frankreichs folgten nach und nach alle europäischen Staaten, und es fehlt nicht mehr viel, um Europa, mit Ausnahme der Türkei und größerer Teile von Spanien sowie der nördlichsten Teile von Rußland, mit allem Aufwand gereifter Geodäsie trigonometrisch aufgenommen und topographisch mappiert anzunehmen. Unter den asiatischen Ländern erfreuen sich Japan, Ostindien, unter den amerikanischen die Union, Britisch-Nordamerika und Mexiko des allmählichen Zustandekommens guter Spezialkarten. Für genaue Aufnahme der Küstenstriche aller Ozeane wirken in erster Linie die britische Admiralität, in zweiter die nordamerikanische und französische Marine. Tausende von Seekarten und von topographischen Sektionen beweisen die überall erwachte Tätigkeit von Marinen, der Generalstäbe und Ingenieur-Geographenkorps. Selbstverständlich ist dieser Umschwung nicht ohne Einfluß auf die Privatindustrie geblieben, und es kann auf die Leistungen der geographischen Institute zu Gotha, Berlin, Leipzig und Glogau, auf die Produktion vieler Verleger von London, Paris, Berlin, Petersburg etc., auf die zahlreichen Karten in den Mitteilungen der verschiedenen geographischen Gesellschaften hingewiesen werden, um die Überzeugung zu erlangen, daß die Kartographie beschleunigt in allen Richtungen fortschreitet. Nicht nur der Gelehrte, der Forscher, der Militär, auch der Geschäftsmann und selbst die lange vernachlässigte Schule finden Befriedigung für ihre mannigfaltigen Bedürfnisse, obgleich noch lange nicht alle Kombinationen erschöpft sind, um den überreichen Stoff dem Fachmann und dem Lernenden mundgerecht zu gestalten.
[Literatur.] Ausführlicher verbreiten sich über Landkartenprojektion die Werke von J. Littrow (»Chorographie«, Wien 1833), A. Germain (Par. 1866, 2 Bde.), Gretschel (Weim. 1873), Tissot (Par. 1881; deutsch bearbeitet von Hammer, Stuttg. 1887), Fiorini (Bologna 1881), Zöppritz (Leipz. 1884; neu bearbeitet von Bludau, 1. Teil, das. 1899), Herz (das. 1885), Hammer (Stuttg. 1889), Breusing (Leipz. 1892), Vital (Wien 1903) und in populärer Bearbeitung Steinhauser (3. Aufl., das. 1887); fortlaufende Berichte über die Fortschritte der Kartenprojektionslehre gibt seit 1882 das »Geographische Jahrbuch« (Gotha); über Terrainzeichnung vgl. die Schriften von Lehmann (Dresd. 1812–16; 5. Aufl. 1843, 2 Tle.), Vogel (Berl. 1828), Bach (Stuttg. 1853), F. Chauvin (Berl. 1854), Streffleur (Wien 1876); über Kartenentwurfslehre im allgemeinen, besonders Kartenkunde, vgl. Zondervan, Allgemeine Kartenkunde (deutsch, Leipz. 1901); Gelcich und Sauter, Kartenkunde (2. Aufl. mit Dinse, das. 1901, in der Sammlung Göschen); über Niveaukarten Aufsätze von Streffleur und Steinhauser (»Mitteilungen der Wiener Geographischen Gesellschaft«, 1855 u. 1857). – Über die Karten des Altertums und Mittelalters findet man Nachrichten in Lelewels »Géographie du moyenâge« (Brüssel 1852–57, 4 Bde.), Santarems »Essai sur l'histoire de la cosmographie et de la cartographie pendant le moyen-âge« (Par. 1849–52, 3 Bde.), Wolkenhauers »Leitfaden der Geschichte der Kartographie« (Bresl. 1895), Miller (»Mappae Mundi«, 6 Hefte, Stuttg. 1895–98). Verzeichnisse der neuern Karten enthalten fortlaufend die »Zeitschrift der Gesellschaft für Erdkunde zu Berlin« (1853, von 1891 ab in der »Bibliotheca geographica«), »Petermanns Mitteilungen« (Gotha 1855 ff.), die Zeitschriften der zahlreichen geographischen Gesellschaften des In- und Auslandes, die »Registrande des Großen preußischen Generalstabs« (Berl. 1858–83, nicht fortgesetzt); vgl. Stavenhagen, Skizze der Entwickelung und des Standes des Kartenwesens des außerdeutschen Europa (Ergänzungsheft 148 von »Petermanns Mitteilungen«, Gotha 1904); für ältere deutsche Erscheinungen dienen Engelmanns »Bibliotheca geographica« (Leipz. 1858), die bis 1850 zurückreicht, H. Berghaus' »Kritischer Wegweiser« (Berl. 1829–35); für gedruckte Erscheinungen aller Zeiten und Länder der »Catalogue of the printed maps, plans and charts of the British Museum« (Lond. 1886). Vgl. auch die Übersicht der topographischen Karten beim Artikel »Landesaufnahme«. Über Landkartenhandel s. d.
http://www.zeno.org/Meyers-1905. 1905–1909.